Số thực là gì? Tính chất, thuộc tính của số thực
Số thực là phần kiến thức rất quan trọng mà chúng ta được học trong bộ môn Toán tại chương trình phổ thông. Trong bài viết này, thietbimaycongnghiep.net sẽ cùng các bạn tổng hợp lại phần kiến thức quan trọng này, từ đó hiểu rõ số thực là gì và các thông tin xoay quanh số thực. Mời các bạn cùng theo dõi bài viết!
Contents
Số thực là gì?
Số thực có tên tiếng Anh là Real numbers, là một tập hợp bao gồm các số dương (1,2,3), số 0, số âm (-1,-2,-3), số hữu tỉ (7/2, -13/23), số vô tỉ (số pi, căn bậc hai).

Trong toán học, số thực là một giá trị đại lượng liên tục và có thể biểu diễn bằng một điểm trên trục số. Số thực là tập hợp gồm cả những số hữu tỉ và vô tỉ, nó có thể là những số siêu việt hoặc đại số.
Tập hợp số thực là gì?
Tập hợp số thực bao gồm số vô tỉ và hữu tỉ. Do đó đây là tập hợp số lớn nhất. Bản chất tập hợp số thực là một tập hợp số vô hạn, nên số lượng các số thực khó có thể đếm được.
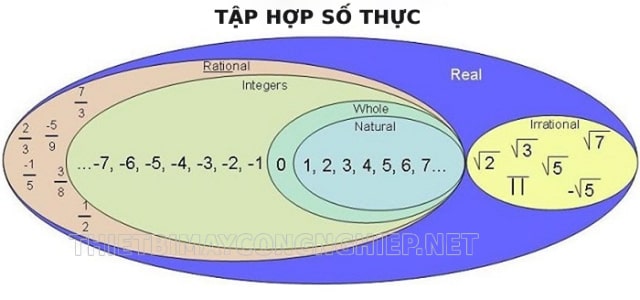
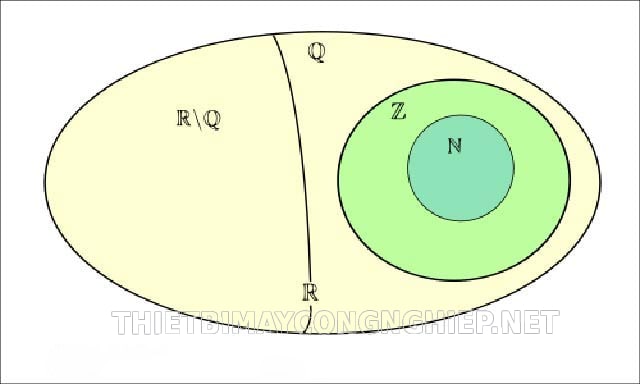
Tập hợp các số thực được ký hiệu R bao gồm:
– Tập hợp các số tự nhiên (ký hiện N): N= {0,1,2,3,…}
– Tập hợp số hữu tỉ (kí hiệu Q): Q= {x= a/b; điều kiện a,b ∈Z và b≠0}.
– Tập hợp số nguyên (ký hiệu Z): Z= {…,-4,-3,-2,-1,0,1,2,3,4,…}
– Tập hợp số vô tỉ (kí hiệu I): I= {số thập phân vô hạn không tuần hoàn ví dụ số pi}.
Tính chất, thuộc tính của số thực
Tính chất số thực

Số thực bao gồm các tính chất như sau:
– Bất kỳ số thực nào đó khác 0 thì sẽ đều là một số âm hoặc một số dương.
– Tổng hoặc tích của hai số thực không âm sẽ là một số thực không âm.
– Tập hợp số thực có vô hạn các số thực, nhiều không thể đếm được.
– Số thực bao gồm hệ thống các tập hợp con vô hạn có thể đếm được.
– Số thực được sử dụng thực hiện các phép đo đại lượng liên tục, do đó có thể biểu diễn được dưới dạng biểu thức thập phân.
Thuộc tính của số thực
Số thực có hai thuộc tính cơ bản quan trọng nhất là cận trên thấp nhất và trường có thứ tự. Trong đó:
– Thuộc tính cận trên thấp nhất: cho biết nếu như tập hợp của một số thực không trống có giới hạn ở trên thì tập này sẽ có cận trên. Ví dụ {1,2,3} có giới hạn trên là 3, do đó nó cận trên là 3.
– Thuộc tính trường có thứ tự cho chúng ta biết các số thực có thể sắp xếp hoàn toàn trên trục hoành theo một cách tương thích với phép cộng, nhân. Điều này có nghĩa là nếu có x,y là hai số thực bất kỳ thì ta sẽ luôn biết được x<y, x>y hay x=y.
Nó sẽ tạo thành một trường có thứ tự, trong đó phép cộng, trừ, nhân hay chia đều có thể thực hiện theo cách tương thích với thứ tự này.
Một số khái niệm liên quan tới số thực

Hằng số thực
Hằng số được biết đến là một đại lượng có giá trị không đổi. Hằng số thực cũng tương tự như thế, nó có nghĩa là một số thực không thay đổi trong mọi tình huống.
Tham số thực
Tham số thực là các số thuộc tập số thực, được coi là phần bị ẩn trong các bài toán số thực.
Giá trị tuyệt đối số thực
Giá trị tuyệt đối số thực là một số bất kỳ, được xác định dựa trên khoảng cách từ điểm mà số đó biểu diễn tới gốc tọa độ. Đặc biệt, giá trị tuyệt đối không được âm và luôn mang tính chất dương.
Biến số thực
Biến số thực ngược lại với hằng số thực, nó là một đại lượng có giá trị bất kỳ và có thể có nhiều giá trị khác nhau. Biến số có thể thay đổi giá trị trong những tình huống khác nhau.
Bài viết trên đã tổng hợp những kiến thức về số thực cơ bản. Mong rằng những chia sẻ trên hữu ích với bạn, giúp bạn vận dụng hiệu quả vào quá trình học tập hay nghiên cứu của bản thân.






