Trực tâm là gì? Hướng dẫn xác định trực tâm của tam giác

Trong hình học phẳng và hình học không gian thì trực tâm tam giác chính là kiến thức cơ bản nhất. Nhờ áp dụng tính chất của trực tâm trong tam giác mà các bạn có thể dễ dàng chứng minh các quan hệ của các cạnh, các góc. Hãy cùng chúng tôi tìm hiểu cách xác định trực tâm tam giác là gì cũng như vận dụng giải một số bài tập trong phần này nhé!

Bạn có biết trực tâm là giao điểm của ba đường gì?

Trực tâm là tên gọi của giao điểm của 3 đường cao trong tam giác bất kỳ. tại các góc trong của tam giác, bạn kẻ 3 đường cao đến các cạnh đối diện, 3 đường cao này sẽ cùng đi qua 1 điểm và điểm này chính là trực tâm h của tam giác đó.

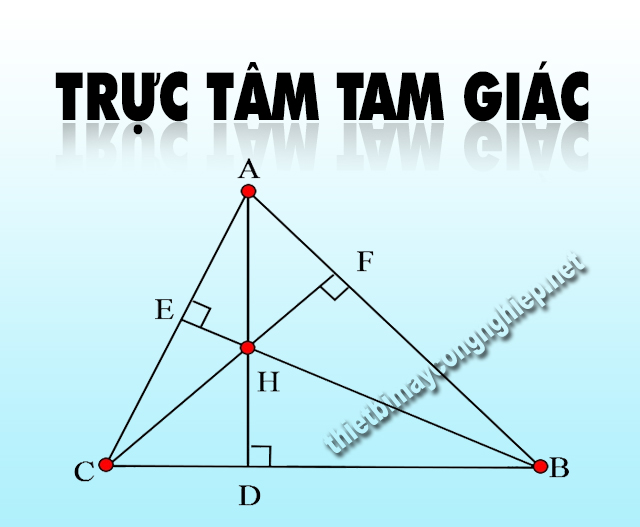
Vậy đường cao của một tam giác là gì? – Theo định nghĩa thì đường cao là đường thẳng từ đỉnh và tạo với cạnh đối diện một góc 90 độ (vuông góc với cạnh đối diện). Cạnh đối diện thường được gọi là đáy tương ứng với cá đường cao đó, còn đường cao là khoảng cách từ đỉnh với đáy – cạnh đối diện.

Giả sử ta có tam giác ABC với AM, BN, CP lần lượt là 3 đường cao của tam giác đó. Gọi O là giao điểm của các đường cao AM, BN, CP. Lúc này, O chính là trực tâm tam giác ABC.

Cách xác định giao điểm của 3 đường cao trong tam giác

Như đã giới thiệu ở trên, chúng ta thấy rằng giao điểm của 3 đường cao chính là trực tâm của tam giác đó. Vì thế, để xác định được điểm này, chúng ta cần xác định được giao điểm của 3 đường cao. Tuy nhiên, bạn không cần kẻ cả 3 đường cao mà chỉ cần vẽ 2 đường cao là có thể xác định được trực tâm trong không gian.

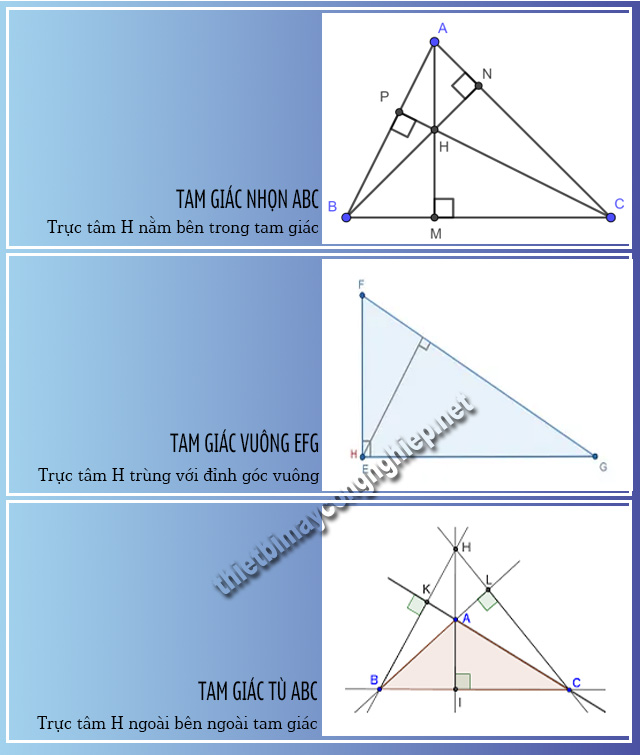
Chúng ta có cách xác định trực tâm giống nhau cho cả 3 loại tam giác (tam giác nhọn, tam giác tù, tam giác vuông). Bằng cách từ 2 đỉnh của tam giác đó, bạn kẻ 2 đường cao từ đỉnh đó đến cạnh đối diện. Hai cạnh đó sẽ giao với nhau tại 1 điểm, tạm gọi là h. Và lúc này h là trực tâm của của tam giác đó, và chắc chắn đường cao từ đỉnh thứ 3 cũng sẽ đi qua h.

Lưu ý về vị trí tương đối của trực tâm trong các loại tam giác là:

• Tam giác nhọn: giao điểm của 3 đường cao sẽ nằm bên trong tam giác.
• Tam giác tù: giao điểm của 3 đường cao sẽ nằm ở bên ngoài tam giác.
• Đặc biệt với tam giác vuông thì 2 cạnh của góc vuông cũng chính là đường cao từ 1 góc nhọn đến cạnh đối diện. Mà 2 đường cao này giao nhau ở góc vuông nên trực tâm của tam giác vuông cũng chính là đỉnh góc vuông.

Một số tính chất cần nhớ của giao điểm 3 đường cao trong tam giác

Các đường và các điểm trong tam giác đều có những tính chất nhất định, đặc biệt là các điểm giao 3 đường trung tuyến, giao của 3 đường trung trực, giao của 3 đường phân giác và giao của 3 đường cao. Vậy trực tâm có tính chất gì thì nó sẽ có 5 tính chất cơ bản sau đây:

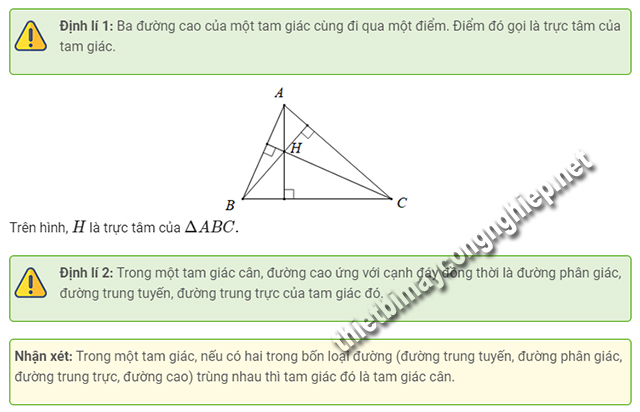
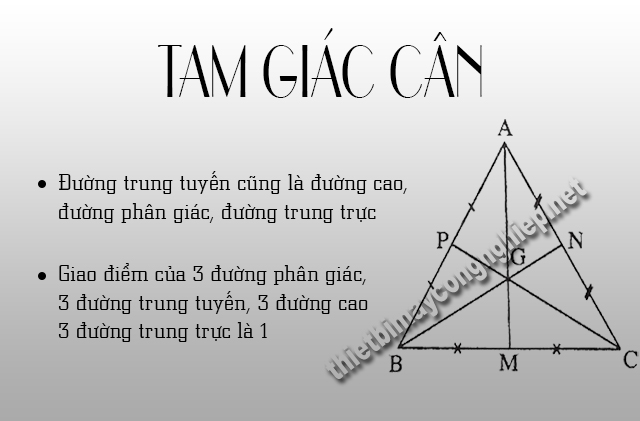
• T/c 1: Trong tam giác cân thì các đường trung trực của tam giác đấy (từ đỉnh ứng với cạnh đáy) cũng đồng thời là đường phân giác, đường cao, đường trung tuyến.
• T/c 2: Nếu một tam giác có đường trung tuyến đồng thời là đường phân giác thì có thể suy ra tam giác đó là tam giác cân.
• T/c 3: Nếu một tam giác có đường trung tuyến cũng là đường đường trung trực thì tam giác đó cân.
• T/c 4: Trực tâm của tam giác nhọn sẽ trùng với tâm của đường tròn nội tiếp tam giác đó (các cạnh của tam giác tiếp xúc với đường tròn).
• T/c 5: Đường cao của tam giác từ một đỉnh sẽ cắt đường tròn ngoại tiếp tam giác đó tại điểm thứ 2 – đối xứng của trực tâm tam giác qua cạnh tương ứng.

⇒ Cũng từ những tính chất trên, người ta rút ra được hệ quả: một tam giác đều thì giao của 3 đường cao, 3 đường phân giác, 3 đường trung trực, 3 đường trung tuyến là 1 điểm đều nằm trong tam giác, cách đều 3 đỉnh, cách đều 3 cạnh.

Hướng dẫn giải bài tập phần trực tâm

Bài tập 58 (SGK Toán 7 tập 2, trang 83):

Giải thích vì sao trực tâm của một tam giác vuông lại trùng với đỉnh góc vuông còn trực tâm của tam giác tù lại nằm ngoài tam giác?

⇒ Đáp án:

Trên đường thẳng d, lấy 3 điểm bất kì I, J, K (I ≠ J ≠ K, J ở giữa I và K). Đường thẳng l vuông góc với d tại J, trên l lấy điểm M (M ≠ J). đường thẳng đi qua I và vuông góc với MK, cắt l tại điểm N. Chứng minh rằng KN ⊥ IM.

⇒ Đáp án:

Lời kết

Vừa rồi, chúng tôi đã tổng hợp các tính chất cũng như hướng dẫn cách để bạn xác định trực tâm của tam giác là gì. hy vọng bài viết đã có thể giải bài tập dễ dàng hơn, nếu bài viết hữu ích, bạn hãy chia sẻ để mọi người cùng nắm được kiến thức này nhé!